Research
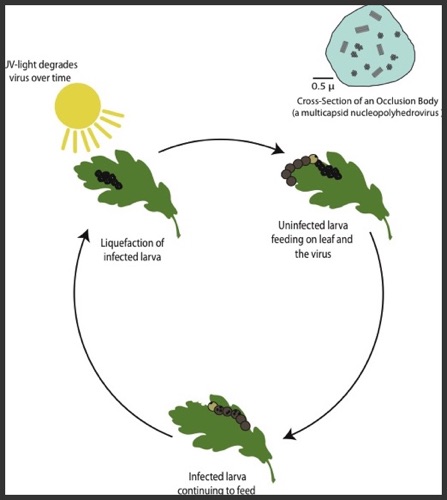
Disease Transmission and Insect Outbreaks
My research efforts in disease ecology center on investigating how biotic and abiotic factors affect disease transmission. Insect diseases such as lepidopteran baculoviruses represent a natural laboratory for the study of transmission dynamics. For instance, baculoviruses are one of the few systems in which transmission can be experimentally measured. These host-pathogen systems also provide a unique testing ground for model development to help guide management practices and understand the mechanisms driving population cycles often seen in these systems.
In this research area, I have focused on answering questions concerning how community structure and environmental stochasticity affect disease dynamics. These questions include the impacts of plant-induced defenses and the effects of evolution of disease resistance on the short-term and long-term population dynamics for an invasive forest pest, the spongy moth (Lymantria dispar) and a crop defoliator, the fall armyworm (Spodoptera frugiperda). I have expanded these questions to examine how different varieties of plant-induced defenses and a changing climate dictate epizootic dynamics and the spatial spread of the other lepidopteran pests. I'm also working on how host-pathogen coevolution determines disease transmission dynamics as the climate continues to warm.
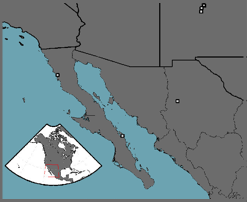
Variability in Disease Transmission
Often the rate at which a disease spreads through a population is quantified by a single number that represents the disease's reproductive rate, Ro, with the assumption that there is no uncertainty associated with this estimate. In fact, there is often a considerable amount of variability associated with disease reproduction, which can have dramatic impacts on disease dynamics and, in turn, host survival. Using data from historical outbreaks of smallpox (see figure for location of Native American outbreaks), I have used Hierarchical Bayesian models to relate parameter uncertainty to uncertainty in model predictions. The results from these studies show that there is dramatic variability in this disease's reproductive rate both within and between populations. By incorporating known variability in epidemic dynamics into policy decisions regarding vaccination strategies, a more well-informed policy choice can be made. Though the above is related to a epidemic, similar methodology can be easily applied to current animal and plant diseases of concern. Currently, I’m applying this methodology to epidemic as well as epizootic outbreaks and the spatial spread of disease.

Population Demography and Viability
Mathematical models can be an important tool for understanding and forecasting population dynamics. An important part of my research has involved the development and analysis of a variety of methods for gauging a population's growth rate and, in turn, viability. At one extreme of complexity, I helped develop a spatially explicit individual-based model for the endangered Cape Sable seaside sparrow (Ammodramus maritimus mirabilis). At the other extreme, I have evaluated methods that use extremely simple count data to perform population viability analysis. Other research endeavors include developing Life-Table Response Experiments (LTREs) for the effects of dams on riparian plant demography. I’ve also been working on the use of Integrated Projection Models (IPMs) in a Bayesian framework. In these demography-related projects, I have examined how best to link empirical data to current theory on population dynamics and to emphasize the importance of the joining of the two to inform conservation decisions.